離散数学 (全36問中6問目)
No.6
値の小さな数や大きな数を分かりやすく表現するために,接頭語が用いられる。例えば,10-3と103を表すのに,それぞれ"m"と"k" が用いられる。10-9と109を表すのに用いられる接頭語はどれか。
出典:平成31年春期 問66
- nとG
- nとM
- pとG
- pとM
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ア
解説
情報処理の世界では、非常に大きい数値や非常に小さい数値を扱うことが多いので、接頭語について理解しておく必要があります。以下の表は、主な接頭語の一覧です。大きい数の接頭語は"k"を除いて大文字、逆に小さい数は小文字が使用されます。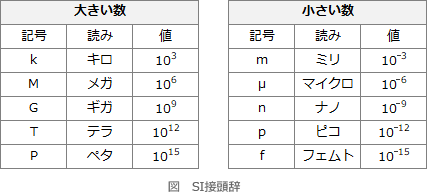 10-9(1/109)を表すのに用いられるのは"n(ナノ)"、109を表すのに用いられるのは"G(ギガ)"です。したがって「ア」の組合せが正解です。
10-9(1/109)を表すのに用いられるのは"n(ナノ)"、109を表すのに用いられるのは"G(ギガ)"です。したがって「ア」の組合せが正解です。

