応用数学 (全12問中2問目)
No.2
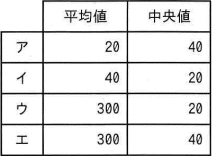
次のデータの平均値と中央値の組合せはどれか。
〔データ〕
10,20,20,20,40,50,100,440,2000
〔データ〕
10,20,20,20,40,50,100,440,2000
出典:令和4年春期 問59
分類
テクノロジ系 » 基礎理論 » 応用数学
正解
エ
解説
データ全体を代表する値として、平均値、中央値、最頻値があります。
10+20+20+20+40+50+100+440+2000=2700
2700÷9=300
【中央値】
設問のデータは既に小さい順に並んでいるので、その中央(9個中5番目)に位置する40
したがって「エ」の組合せが適切です。
- 平均値
- データの値を合計して、その合計値をデータの個数で割った値
- 中央値
- データを値の大小で並べたときに中央に位置する値
※データの個数が偶数のときは中央の値が2つになるので、その2つの平均値 - 最頻値
- データの中で最も多く出現する値
10+20+20+20+40+50+100+440+2000=2700
2700÷9=300
【中央値】
設問のデータは既に小さい順に並んでいるので、その中央(9個中5番目)に位置する40
したがって「エ」の組合せが適切です。