分野：マネジメント系
中分類：プロジェクトマネジメント
小分類：プロジェクトマネジメント

アローダイアグラムは、PERT図とも呼ばれ、工程のスケジュール管理に利用される図です。各作業間の関連性や順序関係を図として表現することで、プロジェクト完了までに必要な期間やクリティカルパスを洗い出すことができます。
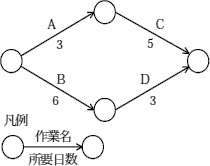
凡例にもあるように、矢印が作業を、○が作業の開始点または終了点を示しています。

このアローダイアグラムにおいて、全体が完了するまでに実施しなくてはならない作業の経路は、

• A(3日)→C(5日)＝8日
• B(6日)→D(3日)＝9日

の2通りがあり、短縮前の段階では、B→Dがクリティカルパスで、作業全体の所要日数は9日ということがわかります。

作業Bを3日，作業Cを1日短縮した後の２つの経路は、

• A(3日)→C(4日)＝7日
• B(3日)→D(3日)＝6日

というように完了日数が変わり、今度はA→Cがクリティカルパス、所要日数は7日ということになります。

したがって所要日数は、9日→7日で2日短縮されることになります。

クリティカルパス

プロジェクトのスケジュールにおいて、遅延することがプロジェクト全体の遅延につながってしまう一連の作業のつながりを示す経路のこと