応用数学(全12問中9問目)
No.9解説へ
表のA列とB列に0から9までの数字のすべての組合せが入っており,全部で100行ある。表からA列の値がB列の値以下である行をすべて取り除く。残りは何行あるか。

出典:平成22年春期 問67
- 40
- 45
- 50
- 55
広告
解説
A列が、1である行と2である行について考えてみると法則がわかります。
[A列が、1の行]
A, B列で表される数値が"10"~"19"において、削除されるのは、"11"~"19"で残る行は"10"の一行だけです。
[A列が、2の行]
A, B列で表される数値が"20"~"29"において、削除されるのは、"22"~"29"で残る行は"20","21"の二行です。
これをA列が、9である行まで続けていった場合に残る行数の合計は、
1+2+3+4+5+6+7+8+9=45
で45行であることがわかります。
※A列が、0の行…A, B列で表される数値が"00"~"09"においては、すべての行でA列の値がB列の値以下になるので一行も残りません。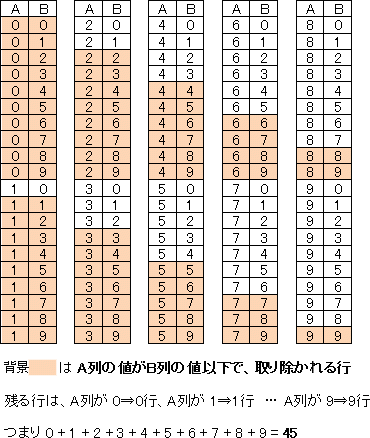
[A列が、1の行]
A, B列で表される数値が"10"~"19"において、削除されるのは、"11"~"19"で残る行は"10"の一行だけです。
[A列が、2の行]
A, B列で表される数値が"20"~"29"において、削除されるのは、"22"~"29"で残る行は"20","21"の二行です。
これをA列が、9である行まで続けていった場合に残る行数の合計は、
1+2+3+4+5+6+7+8+9=45
で45行であることがわかります。
※A列が、0の行…A, B列で表される数値が"00"~"09"においては、すべての行でA列の値がB列の値以下になるので一行も残りません。

広告