オリジナル予想問題1 問36
問36解説へ
下図のアローダイアグラムで表わされる作業を伴うプロジェクトがある。各作業の見直しを行ったところ、作業Cが1日間, 作業Dが3日間の短縮が可能であることが分かった。見直し後このプロジェクト全体の作業日数は、見直し前と比較して、何日間短縮することができるか。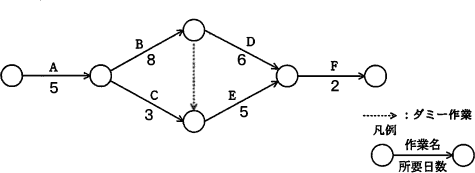

- 1
- 2
- 3
- 4
正解 ア問題へ
広告
解説
まずこのプロジェクトにおけるクリティカルパスを求めます。
[A→B→D→F]
5+8+6+2=21日
[A→C→E→F]
5+3+(B作業完了待ち5日)+5+2=20日
したがって見直し前のクリティカルパスはA→B→D→Fで、最短完了日数は21日とわかります。
作業Cが1日間, 作業Dが3日間の短縮がされると、
[A→B→D→F]
5+8+3+2=18日
[A→C→E→F]
5+2+(B作業完了待ち6日)+5+2=20日
となり、[A→B→D→F]は作業Dが短縮したぶん全体も3日短縮され18日となりますが、[A→C→E→F]では作業Cが短縮しても作業Bの完了待ちが1日増えるだけで全体としての完了日数は変化なく20日です。
したがって見直し後は、クリティカルパスがA→C→E→F、最短完了日数が20日となります。
見直し前後を比べるとプロジェクト全体としては21-20=1で1日の短縮が可能になることがわかります。したがって「ア」が正解です。
[A→B→D→F]
5+8+6+2=21日
[A→C→E→F]
5+3+(B作業完了待ち5日)+5+2=20日
したがって見直し前のクリティカルパスはA→B→D→Fで、最短完了日数は21日とわかります。
作業Cが1日間, 作業Dが3日間の短縮がされると、
[A→B→D→F]
5+8+3+2=18日
[A→C→E→F]
5+2+(B作業完了待ち6日)+5+2=20日
となり、[A→B→D→F]は作業Dが短縮したぶん全体も3日短縮され18日となりますが、[A→C→E→F]では作業Cが短縮しても作業Bの完了待ちが1日増えるだけで全体としての完了日数は変化なく20日です。
したがって見直し後は、クリティカルパスがA→C→E→F、最短完了日数が20日となります。
見直し前後を比べるとプロジェクト全体としては21-20=1で1日の短縮が可能になることがわかります。したがって「ア」が正解です。
広告