離散数学 (全36問中12問目)
No.12
二つの集合AとBについて，常に成立する関係を記述したものはどれか。ここで，(X∩Y)は，XとYの両方に属する部分(積集合)，(X∪Y)は，X又はYの少なくとも一方に属する部分(和集合)を表す。
出典：平成27年春期 問62
- (A∪B)は，(A∩B)でない集合の部分集合である。
- (A∪B)は，Aの部分集合である。
- (A∩B)は，(A∪B)の部分集合である。
- (A∩B)は，Aでない集合の部分集合である。
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ウ
解説
集合Aの全てに要素が集合Bに含まれるとき、AはBの一部分であるという意味で「AはBの部分集合である」といいます。
(A∪B)と(A∩B)をベン図で表現すると以下のようになります。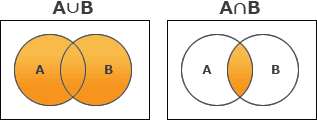
(A∩B)は(A∪B)の一部分になっているので「ウ」が正解です。
(A∪B)と(A∩B)をベン図で表現すると以下のようになります。