離散数学 (全36問中14問目)
No.14
図1のように二つの入力に対し,一つの出力を行うボックスがある。このボックスへの入力は"賛成"か"反対"のいずれかであり,入力が二つとも"賛成"のときだけ"賛成"と出力し,その他のときは"反対"と出力する。図2のように,三つの入力を二つのボックスに入力したときの出力に関する記述のうち,正しいものはどれか。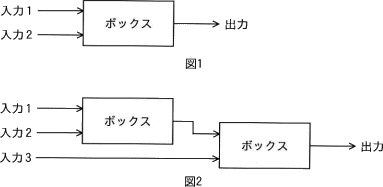

出典:平成26年春期 問57
- 入力が一つ以上"賛成"のときは常に,"賛成"と出力する。
- 入力が二つ以上"賛成"のときは常に,"賛成"と出力する。
- 入力が二つ以上"反対"のときだけ,"反対"と出力する。
- 入力が三つとも"賛成"のときだけ,"賛成"と出力する。
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
エ
解説
設問のボックスは、両方の入力が"賛成"の時にだけ"賛成"を出力するので、図2で最終的な出力が"賛成"となるためには、右のボックスの入力値である"左のボックスの出力"と"入力3"の両方が"賛成"である必要があります。(図中の①)
左のボックスで"賛成"が出力されるには、"入力1"と"入力2"の両方が"賛成"である必要があります。(図中の②)
つまり、最終的に"賛成"が出力されるためには入力のすべてが"賛成"であることが必要条件で、それ以外の場合では"反対"を出力するのが図2の特徴です。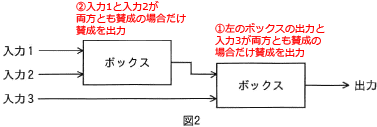 したがって正しい記述は「エ」です。
したがって正しい記述は「エ」です。
左のボックスで"賛成"が出力されるには、"入力1"と"入力2"の両方が"賛成"である必要があります。(図中の②)
つまり、最終的に"賛成"が出力されるためには入力のすべてが"賛成"であることが必要条件で、それ以外の場合では"反対"を出力するのが図2の特徴です。

