応用数学 (全12問中4問目)
No.4
3人の候補者の中から兼任も許す方法で委員長と書記を1名ずつ選ぶ場合，3人の中から委員長1名の選び方が3通りで，3人の中から書記1名の選び方が3通りであるので，委員長と書記の選び方は全部で9通りある。5人の候補者の中から兼任も許す方法で委員長と書記を1名ずつ選ぶ場合，選び方は何通りあるか。
出典：令和元年秋期 問72
- 5
- 10
- 20
- 25
分類
テクノロジ系 » 基礎理論 » 応用数学
正解
エ
解説
5人の中から委員長1名を選ぶ方法は5通り、5人の中から書記1名は5通りです。委員長と書記の兼任が許されているので、委員長の選び方のそれぞれについて書記の選び方が5通りあることになります。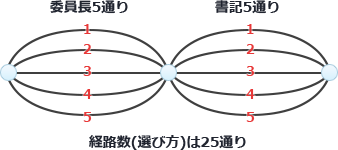
したがって選び方は「5通り×5通り＝25通り」です。
ちなみに、兼任を許さない場合は5人から1名委員長を選び、残った4人から書記1名を選ぶことになるので「5通り×4通り＝20通り」の選び方があります。
ちなみに、兼任を許さない場合は5人から1名委員長を選び、残った4人から書記1名を選ぶことになるので「5通り×4通り＝20通り」の選び方があります。