HOME»ITパスポート平成21年春期»問64
ITパスポート平成21年春期 問64
問64
2進数10110を3倍したものはどれか。
- 111010
- 111110
- 1000010
- 10110000
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ウ
解説
答えを導く方法としてはいくつかの方法がありますが、一度10進数に直して3倍した数値を2進数に戻す方法と、101102を左へ1ビット分シフトさせて101102を足すという方法を説明します。
【一度10進数に直してから2進数に戻す方法】
まず、2進数10110を10進数で表します。各桁の重みをつけて足し合わせるので、以下のように求めます。
24+22+21=16+4+2=22
次に、この10進数22を3倍します。
22×3=66
最後に、10進数66を2で素因数分解して2進数に戻します。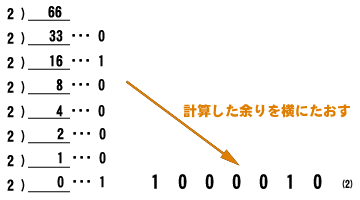 【101102を左へ1ビット分シフトさせて101102を足す方法】
【101102を左へ1ビット分シフトさせて101102を足す方法】
2進数にはビット列全体を1ビット左シフトするごとにその値が2倍になる性質がありますので、101102を左シフトさせて1011002とし、これに101102を足すことで3倍になります。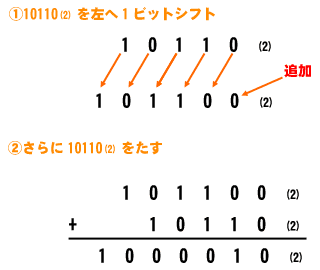
【一度10進数に直してから2進数に戻す方法】
まず、2進数10110を10進数で表します。各桁の重みをつけて足し合わせるので、以下のように求めます。
24+22+21=16+4+2=22
次に、この10進数22を3倍します。
22×3=66
最後に、10進数66を2で素因数分解して2進数に戻します。

2進数にはビット列全体を1ビット左シフトするごとにその値が2倍になる性質がありますので、101102を左シフトさせて1011002とし、これに101102を足すことで3倍になります。

