平成23年特別試験問題 問96
問96解説へ
1日券， 2日券といった日数の異なる種類のチケットの金額計算に対応できるように， (処理内容〕の(2)及び関数の仕様を変更し，引数にチケットの日数を表すM を
追加した。M には使用できる日数が入る。種類別のチケット金額を設定する配列をTP(M， N) とする。Nは大人の場合は1，子供の場合は2とする。配列の値は次のとおりである。引数がJ=10，K=20， M=2のときの合計金額は何円か。
なお，関数は，引数に応じてこの配列を参照し，チケット金額を決定する。
〔配列の値〕
TP(1，1) = 3,000，TP(1，2) = 1,000，
TP(2，1) = 4,000，TP(2，2) = 1,500，
TP(3，1) = 5,000，TP(3，2) = 2,000
追加した。M には使用できる日数が入る。種類別のチケット金額を設定する配列をTP(M， N) とする。Nは大人の場合は1，子供の場合は2とする。配列の値は次のとおりである。引数がJ=10，K=20， M=2のときの合計金額は何円か。
なお，関数は，引数に応じてこの配列を参照し，チケット金額を決定する。
〔配列の値〕
TP(1，1) = 3,000，TP(1，2) = 1,000，
TP(2，1) = 4,000，TP(2，2) = 1,500，
TP(3，1) = 5,000，TP(3，2) = 2,000
- 45,000
- 50,000
- 63,000
- 70,000
正解 ウ問題へ
テクノロジ系
広告
解説
日数Mと、大人・子供を表すNから計算されるチケット金額を保持する配列の内容を表にすると以下のようになります。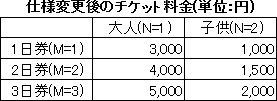
引数 J=10，K=20， M=2を、購入チケットで表すと、2日券の大人用を10枚と2日券の子供用を20枚になります。表から、大人用の2日券は4,000円，子供用の2日券は1,500円であることがわかるので、
4,000×10＋1,500×20 = 70,000
さらにチケットの購入枚数の合計が30枚であり、1割引きの対象となる20枚以上であるので、
70,000×0.9 = 63,000
したがってチケットの合計金額は63,000円になります。
4,000×10＋1,500×20 = 70,000
さらにチケットの購入枚数の合計が30枚であり、1割引きの対象となる20枚以上であるので、
70,000×0.9 = 63,000
したがってチケットの合計金額は63,000円になります。
広告