離散数学 (全36問中22問目)
No.22
16進数のA3は10進数で幾らか。
出典：平成24年秋期 問79
- 103
- 153
- 163
- 179
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ウ
解説
10進数は1桁に0～9の数字を使い10になると桁上がりしますが、16進数は1桁に0～9、A～Fの16個の英数字を使い16になると桁上がりする数値の表現方法です。
10進数の 53 が「10×5＋1×3＝53」であるように、16進数 A3 のAは16の桁、3は1の桁です。上表のとおり16進数のAは10進数の10に対応するので、16の桁が10つ、1の桁が3つということになります。
したがって16進数のA3を10進数に変換した数値は、
16×10＋1×3＝163
したがって「ウ」が正解です。
【別解】
16進数を10進数に変換する場合は、16進数→2進数→10進数というように2進数を経由して解くこともできます。
まず16進数のA3を2進数で表すと、"A"が2進数で1010、"3"は2進数で0011なので、
A3(16) → 1010 0011(2)
となります。2進数の各桁と10進数は下図のように対応しているので、
27＋25＋21＋20＝128＋32＋2＋1＝163
こちらでも163になります。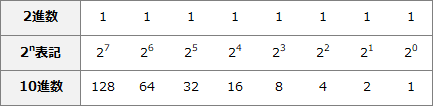
したがって16進数のA3を10進数に変換した数値は、
16×10＋1×3＝163
したがって「ウ」が正解です。
【別解】
16進数を10進数に変換する場合は、16進数→2進数→10進数というように2進数を経由して解くこともできます。
まず16進数のA3を2進数で表すと、"A"が2進数で1010、"3"は2進数で0011なので、
A3(16) → 1010 0011(2)
となります。2進数の各桁と10進数は下図のように対応しているので、
27＋25＋21＋20＝128＋32＋2＋1＝163
こちらでも163になります。