応用数学 (全12問中7問目)
No.7
図1のA1地点からC2地点へ行くとき，通過する地点が最も少なくて済む最短経路は，図2のように数えることによって3通りであることが分かる。A1地点から，C2地点を経由して，D4地点へ行く最短経路は何通りあるか。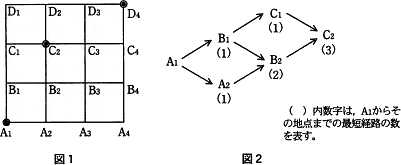
出典：平成22年秋期 問72
- 6
- 9
- 12
- 20
分類
テクノロジ系 » 基礎理論 » 応用数学
正解
イ
解説
A1地点からC2地点まで3通りの経路があります。A1地点からC2地点までと、C2地点からD4地点までは進む方向が変わっているだけですので、C2地点からD4地点までの最短経路数は、A1地点からC2地点までと同様に3通りであることがわかります。設問の右図のように数えれば以下のようになります。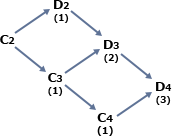
A1地点からC2地点までの3通りの経路をm1, m2, m3、C2地点からD4地点までの3通りの経路をn1, n2, n3 とすると、
m1→C2→n1
m1→C2→n2
m1→C2→n3
m2→C2→n1
…
m3→C2→n3
というように、A1地点からC2地点までの3通りのそれぞれに対して、C2地点からD4地点までの3通りがあることになるので、A1地点から、C2地点を経由して、D4地点へ行く最短経路数は「3通り×3通り＝9通り」と計算できます。したがって「イ」が正解です。
m1→C2→n1
m1→C2→n2
m1→C2→n3
m2→C2→n1
…
m3→C2→n3
というように、A1地点からC2地点までの3通りのそれぞれに対して、C2地点からD4地点までの3通りがあることになるので、A1地点から、C2地点を経由して、D4地点へ行く最短経路数は「3通り×3通り＝9通り」と計算できます。したがって「イ」が正解です。