アルゴリズムとプログラミング (全23問中8問目)
No.8
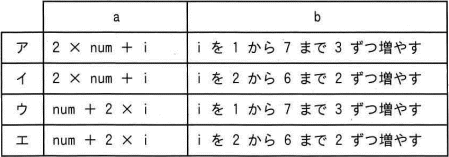
関数 calcX と関数 calcY は,引数 inData を用いて計算を行い,その結果を戻り値とする。関数 calcX を calcX(1) として呼び出すと,関数 calcX の変数 num の値が,1→3→7→13と変化し,戻り値は13となった。関数 calcY を calcY(1) として呼び出すと,関数 calcY の変数 num の値が,1→5→13→25と変化し,戻り値は25となった。プログラム中のa,bに入れる字句の適切な組合せはどれか。

出典:令和4年春期 問96
分類
テクノロジ系 » アルゴリズムとプログラミング » アルゴリズムとプログラミング
正解
エ
解説
空欄aに当てはまる字句から考えていきます。
選択肢は2×num+iとnum+2×iの2つですが、変数 i が1→2→3と増えたとき、変数 num の値がどう変わるかをトレースしていくと以下のようになります。
[2×num+i]
i=1のとき、2×1+1=3 → num
i=2のとき、2×3+2=8 → num
i=3のとき、2×8+3=19 → num
[num+2×i]
i=1のとき、1+2×1=3 → num
i=2のとき、3+2×2=7 → num
i=3のとき、7+2×3=13 → num
したがって、変数 num の値が1→3→7→13となるnum+2×iの式が適切であることがわかります。
※増加量はi=1のとき2、i=2のとき4、i=3のとき6なので、変数 num に 2×i を加算していくと考えることもできます。
次に空欄bについて考えます。
選択肢はiを1から7まで3ずつ増やすとiを2から6まで2ずつ増やすの2つですが、〔プログラム2〕のaにnum+2×iを入れてみると、それぞれ次のような処理の流れになります。
[iを1から7まで3ずつ増やす]
i=1のとき、1+2×1=3 → num
i=4のとき、3+2×4=11 → num
i=7のとき、11+2×7=25 → num
[iを2から6まで2ずつ増やす]
i=2のとき、1+2×2=5 → num
i=4のとき、5+2×4=13 → num
i=6のとき、13+2×6=25 → num
したがって、変数 num の値が1→5→13→25となるiを2から6まで2ずつ増やすの繰返し条件が適切であることがわかります。
以上より、適切な組合せは「エ」となります。
選択肢は2×num+iとnum+2×iの2つですが、変数 i が1→2→3と増えたとき、変数 num の値がどう変わるかをトレースしていくと以下のようになります。
[2×num+i]
i=1のとき、2×1+1=3 → num
i=2のとき、2×3+2=8 → num
i=3のとき、2×8+3=19 → num
[num+2×i]
i=1のとき、1+2×1=3 → num
i=2のとき、3+2×2=7 → num
i=3のとき、7+2×3=13 → num
したがって、変数 num の値が1→3→7→13となるnum+2×iの式が適切であることがわかります。
※増加量はi=1のとき2、i=2のとき4、i=3のとき6なので、変数 num に 2×i を加算していくと考えることもできます。
次に空欄bについて考えます。
選択肢はiを1から7まで3ずつ増やすとiを2から6まで2ずつ増やすの2つですが、〔プログラム2〕のaにnum+2×iを入れてみると、それぞれ次のような処理の流れになります。
[iを1から7まで3ずつ増やす]
i=1のとき、1+2×1=3 → num
i=4のとき、3+2×4=11 → num
i=7のとき、11+2×7=25 → num
[iを2から6まで2ずつ増やす]
i=2のとき、1+2×2=5 → num
i=4のとき、5+2×4=13 → num
i=6のとき、13+2×6=25 → num
したがって、変数 num の値が1→5→13→25となるiを2から6まで2ずつ増やすの繰返し条件が適切であることがわかります。
以上より、適切な組合せは「エ」となります。