平成23年特別試験問題 問48
問48解説へ
図のアローダイアグラムにおいて,作業Bが3日遅れて完了した。全体の遅れを1日にするためには,どの作業を何日短縮すればよいか。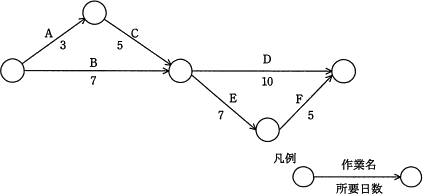

- 作業Cを1日短縮する。
- 作業Dを1日短縮する。
- 作業Eを1日短縮する。
- どの作業も短縮する必要はない。
正解 ウ問題へ
広告
解説
まず図のアローダイアグラムにおいて、プロジェクト開始時におけるクリティカルパスを求めます。
プロジェクト完了に至る一連の作業のつながり(経路)のうち、最も期間を要する経路がクリティカルパスになります。
作業Bが3日遅れたので、クリティカルパスを(作業Bを伴う経路のみ)再計算すると、
前の方の問題(問33)にもありましたが、プロジェクト全体の遅延を取り戻すには、クリティカルパス上の作業を短縮する必要があります。選択肢の方策の中でクリティカルパス上の作業を短縮しているのは「ウ」(作業E)だけなので、これが正解です。
作業Eを1日短縮すると、最短完了日数も一日短縮され21日となり、当初の予定からの遅れを1日だけにすることができます。
プロジェクト完了に至る一連の作業のつながり(経路)のうち、最も期間を要する経路がクリティカルパスになります。
- [A→C→D] 3+5+10=18日
- [B→D] 7+10=17日
- [A→C→E→F] 3+5+7+5=20日
- [B→E→F] 7+7+5=19日
作業Bが3日遅れたので、クリティカルパスを(作業Bを伴う経路のみ)再計算すると、
- [B→D] 10+10=20日
- [B→E→F] 10+7+5=22日
前の方の問題(問33)にもありましたが、プロジェクト全体の遅延を取り戻すには、クリティカルパス上の作業を短縮する必要があります。選択肢の方策の中でクリティカルパス上の作業を短縮しているのは「ウ」(作業E)だけなので、これが正解です。
作業Eを1日短縮すると、最短完了日数も一日短縮され21日となり、当初の予定からの遅れを1日だけにすることができます。
広告